通常ガウスの法則とは、電場に関する法則ですが、ガウスの法則には、電場以外に磁場に対する法則もあります。ここでは、磁場に対するガウスの法則についての説明になります。
磁場に対するガウスの法則とは、磁場の発散は0となること(モノポールが存在しない)を表しています。
公式は、ガウスの法則の電束密度が磁束密度に置き換わった式に類似しており、
以下の通りとなる。
磁場に対するガウスの法則
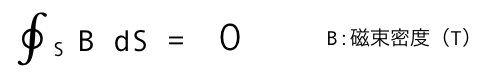
<参考>ガウスの法則
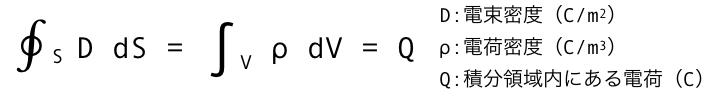
文字で表すと「閉曲面を貫く磁力線は、0である」となる。
意味がわかりませんよね。ここでいう「0」は閉曲面を貫く磁力線の総数が「0」になることを表しています。
これでも、イメージできませんよね。
図を踏まえて説明します。
閉曲面を貫く磁力線は、「閉曲面を流出する磁力線」と「閉曲面に流入する磁力線」があります。前者を(+)、後者を(ー)として下記の図を見てください。

図の「磁石」のように磁力線は、N極からS極へ必ず向かいます。(現時点では、単極の磁性(N、S極のみ)を持つ物質(モノポール)は、発見されていません)
この磁力線の性質から、図の「閉曲面を磁力線が貫く」のように必ず閉曲面を貫く磁力線は、流出(+)すると必ず流入(−)します。
従って、閉曲面を貫く磁力線の流出本数と流入本数は同じ(0になる)となります。

